3. Trigonometry

f. Applications of Trig Functions

3. Slope and Inclination

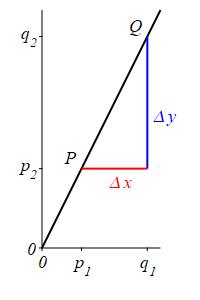
Two points determine a line. Let's consider the line through the points \(P=(p_1,p_2)\) and \(Q=(q_1,q_2)\).
The rise is: \[ \text{rise}=\Delta y=q_2-p_2 \] The run is: \[ \text{run}=\Delta x=q_1-p_1 \] And the slope is: \[ \text{slope}=m=\dfrac{\text{rise}}{\text{run}} =\dfrac{\Delta y}{\Delta x}=\dfrac{q_2-p_2}{q_1-p_1} \]

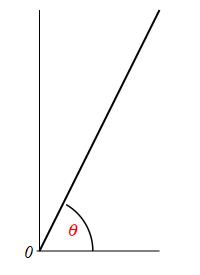
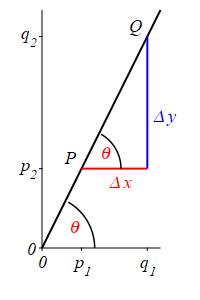
The inclination of a line is the angle \(\theta\) that the line makes with the positive \(x\) direction with the restriction that \(-\,\dfrac{\pi}{2} \le \theta \le \dfrac{\pi}{2}\).

The slope of a line is the tangent of its inclination \[ m=\tan\theta \]

Consider the line through the points \(P=(1,2)\) and \(Q=(4,-4)\). Find the slope, the inclination, the slope-intercept equation of the line and the \(y\)-intercept.

Recall the point-slope equation of the line: \(y=y_0+m(x-x_0)\).

\(m=-2\) \(\theta=-\arctan(2)\approx-1.107\)
\(y=-2x+4\) \(b=4\)

The slope is: \[ m=\dfrac{q_2-p_2}{q_1-p_1}=\dfrac{-4-2}{4-1}=\dfrac{-6}{3}=-2 \] The inclination is: \[ \theta=\arctan(m)=\arctan(-2)=-\arctan(2)\approx-1.107 \] We use the point-slope equation of the line to derive the slope-intercept equation: \[\begin{aligned} y&=p_2+m(x-p_1)=2-2(x-1) \\ &=-2x+4=mx+b \end{aligned}\] So the \(y\)-intercept is \(b=4\).

Consider the line through the points \(P=(2,5)\) with slope \(m=2\). Find the inclination, the slope-intercept equation of the line and the \(y\)-intercept.

\(\theta=\arctan(2)\approx1.107\)
\(y=-\arctan(2)x+2+\arctan(2)\) \(b=2+\arctan(2)\)

The inclination is: \[ \theta=\arctan(m)=\arctan(2)\approx1.107 \] We use the point-slope equation of the line to derive the slope-intercept equation: \[\begin{aligned} y&=p_2+m(x-p_1)=5+2(x-2) \\ &=2x+1=mx+b \end{aligned}\] So the \(y\)-intercept is \(b=1\).

Consider the line through the points \(P=(2,1)\) with inclination \(\theta=60^\circ\). Find the slope, the slope-intercept equation of the line and the \(y\)-intercept.

\(\begin{aligned} m&=\dfrac{\sqrt{3}}{2}\approx.866 \\ y&=\dfrac{\sqrt{3}}{2}x+1-\sqrt{3} \qquad\qquad b=1-\sqrt{3} \end{aligned}\)

The slope is: \[ m=\tan\theta=\tan60^\circ=\dfrac{\sqrt{3}}{2}\approx.866 \] We use the point-slope equation of the line to derive the slope-intercept equation: \[\begin{aligned} y&=p_2+m(x-p_1)=1+\dfrac{\sqrt{3}}{2}(x-2) \\ &=\dfrac{\sqrt{3}}{2}x+1-\sqrt{3}=mx+b \end{aligned}\] So the \(y\)-intercept is \(b=1-\sqrt{3}\).

3. Trigonometry

f. Applications of Trig Functions

3. Slope and Inclination

Heading